Subproject B4 - SFB 901 - On-The-Fly Computing

Subproject B4: Proof-Carrying Services

In this project we investigate techniques for ensuring the quality of services that are procured on the market and assembled on-the-fly, without trusting the service provider. We aim at the development of methods and concepts that allow the consumer of a service to automatically, formally and quickly check if the service possesses the desired properties, i.e., if it adheres to a given specification.

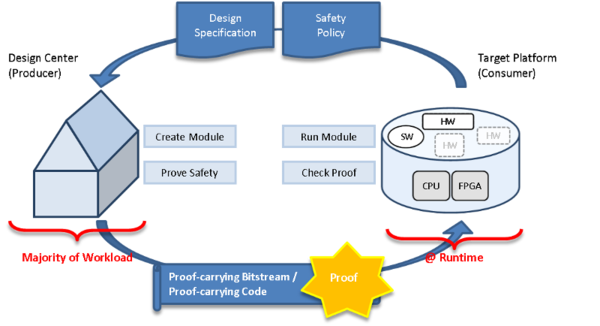
We focussed our research on Proof-carrying Code (PCC) techniques for software services and reconfigurable hardware modules, for the latter referred to as Proof-carrying Hardware (PCH). Our developed methods enable the service provider to automatically derive a formal evidence for the desired quality of a service but its derivation is typically costly. In contrast, the consumer only validates the derived evidence which is computationally less expensive and still ensures rigidly tamper-proof evidence. See Figure 1 for an overview.

Proof-Carrying Code

Current Status

We have improved our existing PCC framework, which is implemented within the configurable verification platform CPAchecker, by integrating additional analysis types and new techniques. Hence, combinations of analyses and analysis refinement strategies such as CEGAR (Counterexample-Guided Abstraction Refinement) have been added to increase the precision of our analyses in order to create reliable certificates. Similarly we upgraded the Programs from Proofs (PfP) framework with focus on data-flow analyses. PfP is an alternative to PCC which uses the analysis information to transform the program into an equivalent program that is more efficient to analyze.
Various optimization have been applied to both frameworks to guarantee low time and memory consumption, in particular, on the consumer side while checking a certificate. To improve further, we explored combinations of verification and testing.

Currently we are adding parts of our research or components of our frameworks to the SFB 901 Proof-of-Concept. This enables Proof-of-Concept participants to on-the-fly verify services before their execution.

Hyperproperties (Work in Progress)

For the near future, we intend to proceed our research in two directions: (1) hyperproperty validation and (2) hierarchical certification.

During the certification of a service, a proof for the validness of certain properties is generated. The proof’s correctness can then be validated with a more efficient checking procedure. In the past the functional properties of interest were trace properties. We intend to investigate the certificate generation and validation of hyperproperties. Hyperproperties, formalized by Clarkson and Schneider in 2010, are a recent noval terminology for generalizing a more complex class of properties. In contrast to trace properties where single program paths sufficies to argue about the properties validness, for hyperproperties such a conclusion can only be taken by consideration of multiple program paths (for example the ‘non-interference’ property in security scenarios or that number of instructions on average respects a certain threshold). Since the research field on hyperproperties is relatively novel, general analysis methods for proving arbitrary hyperproperties are at a beginning stage and the certification of hyperproperties is an open field to tackle.

Hierarchical Certification (Future Work)

Analysis, certificate generation and checking procedures are often tailored to a specific programming language. However, for large-scale real world services these results can be too imprecise, for instance, because of native library calls. The procedure has then three possibilities to handle those native calls: (1) the procedure can give up, (2) the procedure can roughly over-approximate the library call or (3) the procedure can make use of inserted invariants as ground-truth that contain information about these library calls.

Fig. 2: Hierarchical Certification sketch

Building up on (3) we think about enriching invariant solutions using certificates that prove these invariants e.g. for native library calls. In a layered fashion these native libraries can contain custom instruction calls integrated as reconfigurable Hardware modules.

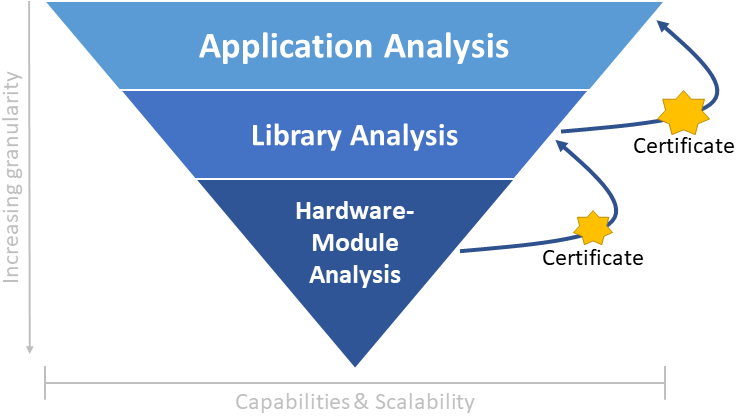
Therefore, we intend the development of a hierarchical certification architecture that can propagate validation results between different layers to increase its precision (cf. Figure 2).

Proof-carrying Hardware

We transferred the idea of Proof-carrying Code to reconfigurable hardware. Proof-carrying hardware cannot only verify functional properties of a hardware service but also non-functional hardware-related properties.

The functional properties can be verified by formulating test functions that use the primary inputs and outputs of the circuit to determine if the desired properties hold.

Our first approach transforms these test functions into an unsatisfiability problem (unSAT) over boolean formulas, which can in many relevant cases be solved quite efficiently using a modern SAT solver. The resolution proof of the unsatisfiability becomes the certificate. For our proof of concept, we use the property of functional equivalence between a circuit implementation and its original specification as a catch-all property, to implement prototypes for Proof-carrying Hardware. We used this approach in particular for combinatorial circuits and sequential circuits with a fixed number of cycles. Due to the closed nature of FPGA vendor’s tools, we cannot use the configurations of actual FPGAs directly. Hence, for demonstration purposes we started with configuration bitstreams for an abstract FPGA. To create real prototypes for PCH, we extended our approach to use virtual FPGA overlays on top of real FPGAs that we can program using open source tool flows compatible with PCH.

To speed up the validation of the resolution proof, we have investigated implementing the validation in hardware itself, which revealed that the hardware solution can be competitive despite potentially large proof sizes and highly irregular access patterns necessary for validation, if a special memory interface like Hybrid Memory Cube is available.

We have also looked into guaranteeing non-functional properties of hardware circuits using PCH, which include the physical aspects of the hardware device and the hardware service that is implemented on the reconfigurable device. Since many of these physical aspects are malleable when using our virtual overlays, or behave non-deterministically because of the dependence on the physical synthesis of the overlay in addition to the virtual synthesis, we have first developed a solution for the worst-case completion time of sequential run-to-completion circuits, as this abstracts the non-determinism away in the clock frequency used for the virtual circuit. We have successfully created certificates for the invariant adherence of a circuit to a given cycle limit.

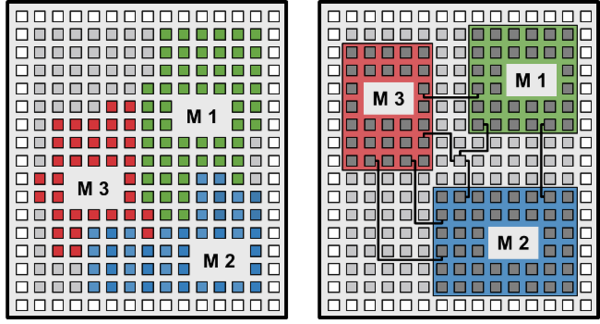
Reconfigurable platforms can greatly benefit from the verification of such non-functional, possibly security-critical features. In Figure 2 below, we depict two FPGA chips with three IP cores, as another example which we are currently investigating. Without placement constraints, the cores are placed in a way that may overlap and allows the individual modules to share resources on the chip, which allows for unintended data leaks and malicious data manipulation. The placement and routing on the right is performed under constraints that physically isolate the individual modules and thereby protect the integrity and confidentiality of their data. With isolated IP cores, the FPGA chip can simultaneously run multiple IP cores with different trust levels without compromising the security of the platform or the data.

Fig. 3: FPGA chip without and with physical isolation

We developed an alternative PCH approach to better verify sequential circuits. It uses IC3 to build an inductive invariant, an overapproximation of the circuit’s state space. The inductive invariant, a logical formula representing a strengthening of the circuit property, is the certificate.

We also started to combine PCH with monitoring and enforcement. The idea is that monitoring and enforcement modules are added to the circuits, to make sure that they exhibit only certain behaviour or properties. PCH is then used to ensure the correct implementation of the added modules which is simpler than ensuring the correctness of the complete and complex circuit. We are currently researching ways to efficiently generate such monitoring modules from formal properties and to check not only the behaviour of the additional modules but also that they are integrated in a way that they cannot be bypassed.

Our goal is to unify our two research branches into a common Proof-Carrying technique for services covering software and hardware aspects. We think of services which execute parts of the service on standard processor hardware and other parts on (reconfigurable) hardware particularly developed for that service. For example, the software service may also execute special, non-standard instructions, so called custom instructions, or call methods implemented in hardware.

In a first step, we started to connect software and hardware verification. For our scenario, we extracted from software verification, the required functionality for the hardware implementation. We considered three techniques which differ in the effort and the reusability of hardware verification. First, we prove functional equivalence, i.e., if the hardware implementation adheres to its specification. Second, we check if the hardware adheres to the rules of the abstract domain used by the software verification. Third, we extract the hardware requirements from the proof of the software verification.

In our ongoing research we want to systematically study our combined hardware and software verification and extend it to a complete Proof-carrying technique. Therefore, we consider the following research questions:

Which kinds of hardware implementations are covered by our approach? For example, can we deal with loops or memory access?
Which software analyses can be used and how complex may they become?
How can we simplify the hardware requirements produced by the software verification?
How to close the gap between the requirements produced by software verification and the representation for hardware verification?
How to automate the translation from extracted software requirements to hardware requirements in a sound way?
What else must be done to automate the combined approach?
How to integrate our existing Proof-carrying Code and Proof-carrying Hardware approaches?

Further Information

For further information, please consult our publications or contact our researchers.

Further information:

Subproject B4 Researchers Publications Theses